Membrane Potentials

Note: An 18-minute mini-lecture on this topic can be viewed at the end of this page.

If a voltmeter is attached to the two terminals of a battery, a voltage difference will be measured across the two terminals. Likewise, if a voltmeter is used to measure voltage across the cell membrane (inside versus outside) of cardiomyocytes, it will be found that the inside of the cell has a negative voltage (measured in millivolts; mV) relative to the outside of the cell (which is referenced as 0 mV). Under resting conditions, this is called the resting membrane potential. With appropriate stimulation of the cell, this negative voltage inside the cell (negative membrane potential) may transiently become positive (become depolarized) owing to the generation of an action potential. Membrane potentials result from a separation of positive and negative charges (ions) across the membrane, similar to the plates within a battery that separate positive and negative charges.

Membrane potentials in cells are determined primarily by three factors: 1) the concentration of ions on the inside and outside the cell; 2) the permeability of the cell membrane to those ions (i.e., ion conductance) through specific ion channels; and 3) by the activity of electrogenic pumps (e.g., Na⁺/K⁺-ATPase and Ca⁺⁺ transport pumps) that maintain the ion concentrations across the membrane.

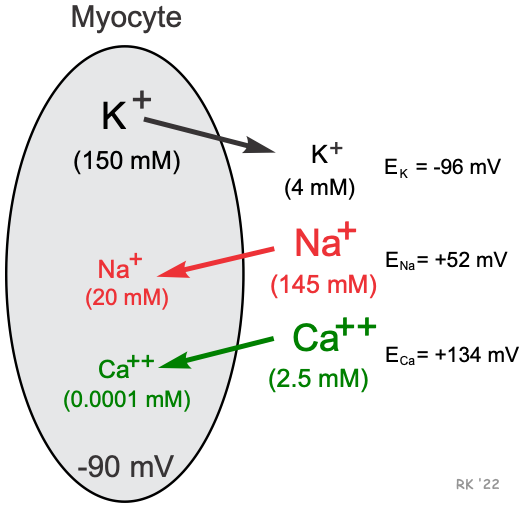Cardiac cells, like all living cells, have different concentrations of ions across the cell membrane, the most important of which are Na⁺, K⁺, Cl^-, and Ca⁺⁺ (see figure to right). There are also negatively charged proteins within the cell to which the cell membrane is impermeable. In a cardiac cell, the concentration of K⁺ is high inside the cell and low outside. Therefore, there is a chemical gradient for K⁺ to diffuse out of the cell. The opposite situation is found for Na⁺ and Ca⁺⁺ where their chemical gradients (high outside, low inside concentrations) favor an inward diffusion. 

Potassium ion

To understand how a membrane potential is generated, first consider a hypothetical cell in which K⁺ is the only ion across the membrane apart from the large negatively charged proteins inside the cell. Because the cell has potassium channels through which K⁺ can move in and out of the cell, K⁺ diffuses down its chemical gradient (out of the cell) because its concentration is much higher inside the cell than outside. As K⁺ (a positively charged ion) diffuses out of the cell, it leaves behind negatively charged proteins. This leads to a separation of charges across the membrane and therefore a potential difference across the membrane. Experimentally, it is possible to prevent the K⁺ from diffusing out of the cell. This can be achieved by applying a negative charge to the inside of the cell that prevents the positively charged K⁺ from leaving the cell. The negative charge across the membrane that would be necessary to oppose the outward movement of K⁺ down its concentration gradient is termed the equilibrium potential for K⁺ (E_K; Nernst potential). The Nernst potential for K⁺ can be calculated as follows:

(where [K⁺]_i = 150 mM and [K⁺]_o = 4 mM; and z=1 because K⁺ is monovalent)

The E_K represents the electrical potential necessary to keep K⁺ from diffusing out of the cell, down its chemical gradient. If the outside K⁺ concentration is increased from 4 to 40 mM, then the chemical gradient driving K⁺ out of the cell would be reduced; therefore, the membrane potential required to maintain electrochemical equilibrium (E_K) would be less negative according to the Nernst relationship. In this example, the E_K becomes -35 mV when the outside K⁺ concentration is 40 mM. In other words, when K⁺ is elevated 10-fold outside the cell, the chemical gradient driving K⁺ out of the cell is reduced, and therefore a less negative voltage is required to keep K⁺ from diffusing out of the cell.

The resting potential for a ventricular myocyte is about -90 mV, which is near the equilibrium potential for K⁺ when extracellular K⁺ concentration is 4 mM. Since the equilibrium potential for K⁺ is -96 mV and the resting membrane potential is -90 mV, there is a net electrochemical driving force (difference between membrane potential and equilibrium potential) of 6 mV acting on the K⁺. The membrane potential is more positive than the equilibrium potential, and therefore the net driving force is outward because of K⁺ having a positive charge. Because the resting cell has a finite permeability to K⁺ and the presence of a small net outward driving force acting upon K⁺, there is a slow outward leak of K⁺ from the cell. If K⁺ continued to leak out of the cell, its chemical gradient would be lost over time; however, a Na⁺/K⁺-ATPase pump brings the K⁺ back into the cell and to maintain the K⁺ chemical gradient.

Sodium and calcium ions

Because the Na⁺ concentration is higher outside the cell, this ion diffuses down its chemical gradient into the cell. Experimentally, this inward diffusion of Na⁺ can be prevented by applying a positive charge to the inside of the cell. When this positive change counterbalances the chemical diffusion force driving Na⁺ into the cell, there will be no net movement of Na⁺ into the cell, and Na⁺ will therefore be in electrochemical equilibrium. The membrane potential required to produce this electrochemical equilibrium is called the equilibrium potential for Na⁺(E_Na) and is calculated by:

(where [Na⁺]_i = 20 mM and [Na⁺]_o = 145 mM; and z=1 because Na⁺ is monovalent)

The positive E_Na means that to balance the inward directed chemical gradient for Na⁺, the cell interior needs to be +52 mV to prevent Na⁺ from diffusing into the cell. At a resting membrane potential of -90 mV, there is not only a large chemical driving force, but also a large electrical driving force acting upon external Na⁺ to cause it to diffuse into the cell. The difference between the membrane potential and the equilibrium potential (-142 mV) represents the net electrochemical force driving Na⁺ into the cell at resting membrane potential. At rest, however, the permeability of the membrane to Na⁺ is very low so that only a small amount of Na⁺ leaks into the cell. During an action potential, the cell membrane becomes more permeable to Na⁺, which increases sodium entry into the cell through sodium channels. At the peak of the action potential in a cardiac cell (e.g., ventricular myocyte), the membrane potential is approximately +20 mV. Therefore, while the resting potential is far removed from the E_Na, the peak of the action potential approaches E_Na. Because a small amount of Na⁺ enters the cell at rest, and a relatively large amount of Na⁺ enters during action potentials, a Na⁺/K⁺-ATPase pump is required to transport Na⁺ out of the cell (in exchange for K⁺) to maintain the chemical gradient for Na⁺.

Similar to Na⁺, there is a large Ca⁺⁺ concentration difference across the cell membrane. Therefore, Ca⁺⁺ diffuses into the cell, which occurs through calcium channels. Applying the Nernst equation to external and internal calcium concentrations of 2.5 mM and 0.0001 mM, respectively, results in an equilibrium potential of +134 mV, as shown below.

This value also includes that the fact that Ca⁺⁺ is a divalent instead of a monovalent cation; therefore, the -61 constant in the above equation is divided by 2 because z = 2 (z = number of charges). Because the equilibrium potential is much more positive than the resting membrane potential, there is a net electrochemical force trying to drive Ca⁺⁺ into the cell, which occurs when calcium channels open.

The above discussion indicates how changes in the concentration of individual ions across the membrane can alter the membrane potential. However, to fully understand how multiple ions affect the membrane potential, and ultimately, how the membrane potential changes during action potentials, it is necessary to learn how changes in membrane ion conductance affect the membrane potential. Furthermore, electrogenic ion pumps such as the Na⁺/K⁺-ATPase pump contribute to the membrane potential as they transport ions across the membrane to maintain the ion concentrations across the membrane.

The following is a mini-lecture on cardiac membrane potentials (18.3 minutes):

Revised 10/27/2023