Velocity versus Flow of Moving Blood
The terms "velocity" and "flow" can sometimes be confused and thought of as being interchangeable, but they are not. Velocity is the distance an object (solid, liquid, or gas) moves with respect to time (i.e., the distance traveled per unit of time). With blood flowing in a vessel, velocity is often expressed in the units of cm/sec. In contrast, flow is the volume of a liquid or gas that is moving per unit of time. For blood flowing in a large vessel, flow is typically expressed in the units of mL/min (cm3/min; 1 mL = 1 cm3). The flow of blood in a vessel is related to velocity by the following equation:
F = V · A
(F = flow, V = mean velocity, and A = cross-sectional area of the vessel)
It is important to use the mean velocity of the moving blood because blood flowing in a vessel has a parabolic profile under laminar flow conditions. Therefore, the mean velocity will be a value less than the maximal centerline velocity in a vessel.
The cross-sectional area of a vessel (A) equals pi (π) times the radius squared (π ⋅ r2), or A= r2. Therefore, the relationship between flow and velocity can be expressed as:
F ∝ V · r2
This relationship shows that, at a constant vessel radius, changes in flow are proportionate to changes in velocity, and vice versa.
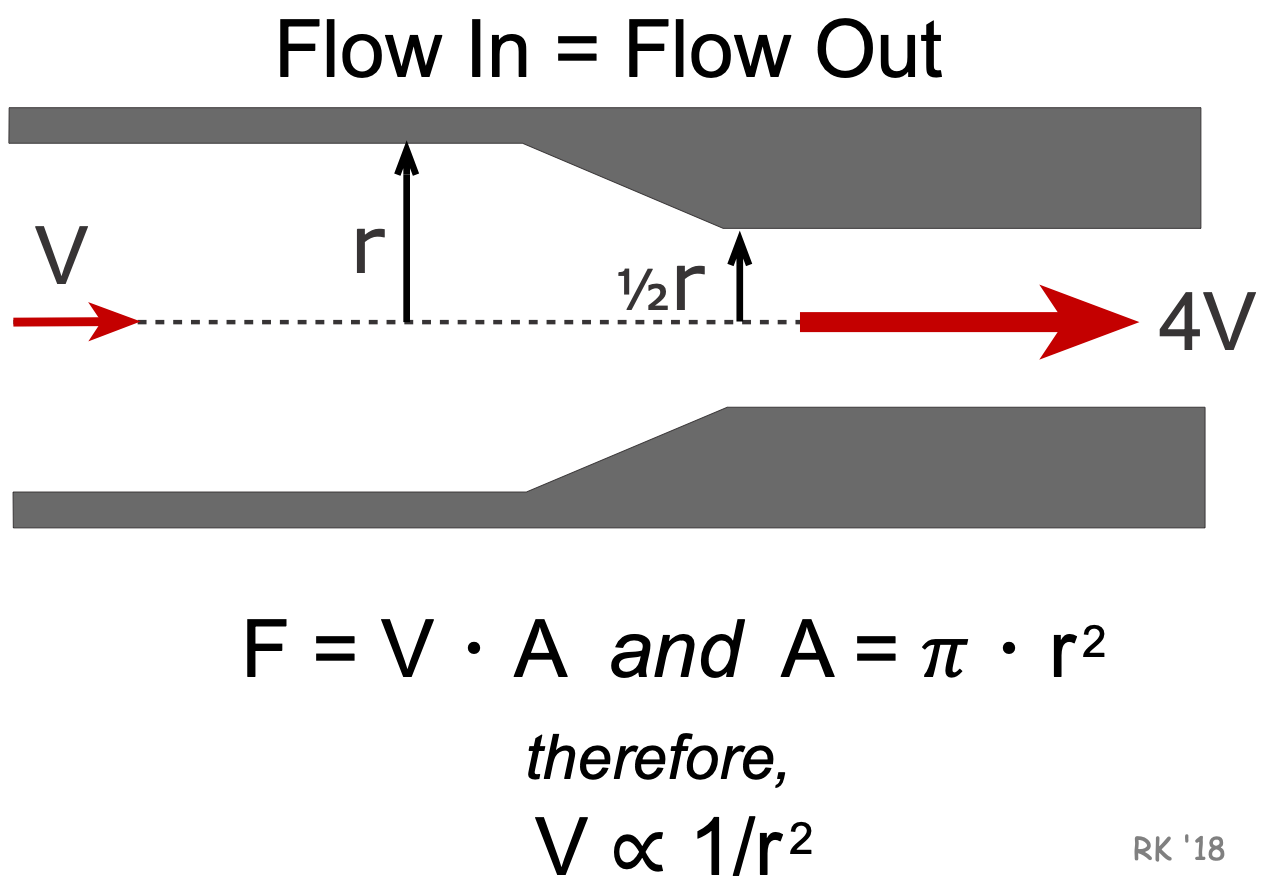 Another important relationship is that velocity, at constant flow, is inversely related to the radius squared (V ∝ 1 / r2 at constant flow). In the example shown in the figure, reducing the radius by 50% causes the velocity to increase 4-fold at constant flow. This relationship has significant implications for turbulent flow and the Bernoulli effect. It is important not to draw the conclusion from the above relationship that flow is proportionate to radius squared. The relationship between flow and radius for a fluid flowing in a tube is much more complex and is described by Poiseuille's relationship.
Another important relationship is that velocity, at constant flow, is inversely related to the radius squared (V ∝ 1 / r2 at constant flow). In the example shown in the figure, reducing the radius by 50% causes the velocity to increase 4-fold at constant flow. This relationship has significant implications for turbulent flow and the Bernoulli effect. It is important not to draw the conclusion from the above relationship that flow is proportionate to radius squared. The relationship between flow and radius for a fluid flowing in a tube is much more complex and is described by Poiseuille's relationship.
As a practical application of the above relationships, the use of hemodynamic data obtained from Doppler measurements must be carefully interpreted. Doppler techniques measure the velocity of the flowing blood, not flow per se. If a Doppler measurement shows that velocity decreases (for example in a brachial artery) under two different conditions (e.g., before and after administration of a vasoactive drug), the only way to know for sure that the change in velocity represents a proportionate change in flow is to know that the intervention did not alter vessel diameter. In fact, a situation could occur in which velocity falls, but flow is increased. This could occur if the vasoactive drug dilates the artery from which the velocity is being measured and slightly dilates vessels downstream. The dilated brachial artery would cause a fall in velocity within the brachial artery; however, the downstream vasodilation could cause total flow to increase because of the series relationship of the vasculature. Another example would be using a Doppler technique to measure velocity in a stenotic region of a peripheral artery. Here, the velocity in the region of the stenosis will be very high, yet the flow will probably be reduced.
Revised 11/05/2023
 Cardiovascular Physiology Concepts, 3rd edition textbook, Published by Wolters Kluwer (2021)
Cardiovascular Physiology Concepts, 3rd edition textbook, Published by Wolters Kluwer (2021) Normal and Abnormal Blood Pressure, published by Richard E. Klabunde (2013)
Normal and Abnormal Blood Pressure, published by Richard E. Klabunde (2013)