The Bernoulli Principle and Energetics of Flowing Blood
Because flowing blood has mass and velocity, it has kinetic energy (KE). This KE is proportionate to the mean velocity squared (V2; from KE = ½ mV2). As the blood flows inside a vessel, pressure is exerted laterally against the walls of the vessel; this pressure represents the potential or pressure energy (PE). The total energy (E) of the blood flowing within the vessel, therefore, is the sum of the kinetic and potential energies (assuming no gravitational effects) as shown below.
E = KE + PE
Since KE ∝ V2), then E ∝ V2 + PE
There are two important concepts that follow from this relationship.
- Blood flow is driven by the difference in total energy between two points. Although pressure is normally considered as the driving force for blood flow, it is the total energy (KE + PE) that drives flow between two points (e.g., longitudinally along a blood vessel or across a heart valve). Throughout most of the cardiovascular system, KE is low, so for practical reasons, it is frequently stated that the pressure energy (PE) difference drives flow. When KE is high, however, adding KE to the PE significantly increases the total energy, E. To illustrate this, consider the flow across the aortic valve during cardiac ejection. Late during ejection, the intraventricular pressure (PE) falls slightly below the aortic pressure (PE). Nevertheless, flow continues to be ejected into the aorta. This is because the KE of the blood as it moves across the valve at a very high velocity ensures that the total energy (E) in the blood crossing the valve is higher than the total energy of the blood more distal in the aorta.
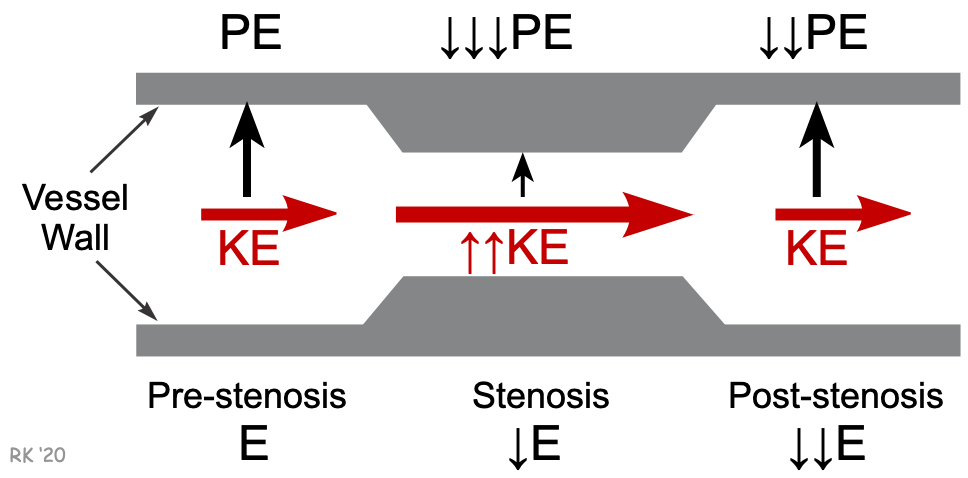
- Kinetic energy and pressure energy can be interconverted so that total energy remains unchanged. This is the basis of the Bernoulli principle. This principle can be illustrated by a blood vessel that is suddenly narrowed, then returned to its normal diameter. In the narrowed region (stenosis), the velocity increases as the diameter decreases. Quantitatively, V ∝ 1/D2 because flow (F) is the product of mean velocity (V) and vessel cross-sectional area (A) (F = V · A, continuity equation), and A is related directly to diameter (D) (or radius, r) squared (from A = π r2). If the diameter is reduced by one-half in the region of the stenosis, the velocity increases 4-fold. Because KE ∝ V2, the KE increases 16-fold. Assuming that the total energy is conserved within the stenosis (E decreases because of resistance, as shown in the figure), then the 16-fold increase in KE must cause a reciprocal decrease in the magnitude of PE. The fall in PE represents a decrease in the lateral pressure against the vessel walls. Therefore, an increase in velocity leads to a decrease in lateral pressure, which is the basis for the Venturi effect. Once past the narrowed segment, KE reverts to its pre-stenosis value because the post-stenosis diameter is the same as the pre-stenosis diameter and flow (and therefore, velocity) is conserved. Because of the stenosis, turbulence likely occurs, and therefore the post-stenosis PE and E will both fall (energy losses due to increased friction). To summarize this concept, blood flowing at higher velocities has a higher ratio of kinetic energy to potential (pressure) energy.
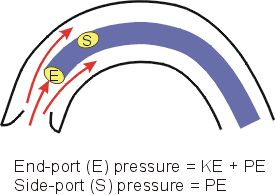 An application of the Bernoulli principle is found when blood pressure measurements are made from within the ascending aorta. As described above, during ventricular ejection, the velocity and hence the kinetic energy of the flowing blood are very high. The instantaneous blood pressure that is measured within the aorta will be significantly different depending on how the pressure is measured. As illustrated in the figure, if a catheter has an end-port (E) sensor that is facing the flowing stream of blood, it will measure a pressure that is significantly higher than the pressure measured by a side-port (S) sensor on the same catheter. The reason for the discrepancy in measured pressures is that the end-port measures the total energy of the flowing blood. As the flow of blood presses against the end of the catheter, the kinetic energy is converted to potential (or pressure) energy, and added to the existing potential energy, increasing the pressure energy. The side-port will not be pressed against by the flowing stream, so kinetic energy is not converted to potential energy. The side-port sensor, therefore, only measures the potential energy, which is the lateral pressure acting on the walls of the aorta. The difference between the two types of pressure measurements can range from a few mmHg to over 20 mmHg, depending on the peak velocity of the flowing blood within the aorta.
An application of the Bernoulli principle is found when blood pressure measurements are made from within the ascending aorta. As described above, during ventricular ejection, the velocity and hence the kinetic energy of the flowing blood are very high. The instantaneous blood pressure that is measured within the aorta will be significantly different depending on how the pressure is measured. As illustrated in the figure, if a catheter has an end-port (E) sensor that is facing the flowing stream of blood, it will measure a pressure that is significantly higher than the pressure measured by a side-port (S) sensor on the same catheter. The reason for the discrepancy in measured pressures is that the end-port measures the total energy of the flowing blood. As the flow of blood presses against the end of the catheter, the kinetic energy is converted to potential (or pressure) energy, and added to the existing potential energy, increasing the pressure energy. The side-port will not be pressed against by the flowing stream, so kinetic energy is not converted to potential energy. The side-port sensor, therefore, only measures the potential energy, which is the lateral pressure acting on the walls of the aorta. The difference between the two types of pressure measurements can range from a few mmHg to over 20 mmHg, depending on the peak velocity of the flowing blood within the aorta.
Revised 01/21/2024
 Cardiovascular Physiology Concepts, 3rd edition textbook, Published by Wolters Kluwer (2021)
Cardiovascular Physiology Concepts, 3rd edition textbook, Published by Wolters Kluwer (2021) Normal and Abnormal Blood Pressure, published by Richard E. Klabunde (2013)
Normal and Abnormal Blood Pressure, published by Richard E. Klabunde (2013)